NumPy

Learning goals

After finishing this chapter, you are expected to

• be able to import packages

• use index and slicing in NumPy

• use common NumPy functions

Source

This chapter includes figures from NumPy: the absolute basics for beginners page on the NumPy website.

Modules and packages

By now, you know how to write a function and you know that Python has a set of built-in functions. The list of built-in functions in Python is very short, yet Python is a very powerful and popular programming language. The reason for this is that Python provides modules and packages that significantly extend the basic functionality. In this chapter, you will for the first time use one of these packages, namely the NumPy package. For many practical programming problems, you’ll need vectors and matrices, or arrays. The most common way to work with such objects in Python is using the NumPy package. NumPy is the workhorse for anything related to vectors and matrices, offers a wide range of functions, and provides the ndarray object that represents multidimensional matrices and is at the core of many packages in Python. This package comes preinstalled with Anaconda, so you don’t have to install anything else.

Selecting the right interpreter

Please make sure that you’re using the right interpreter in VS Code! On the bottom right of your screen, it says something like ‘3.9.12’. This is the Python interpreter you’re using. Click on it and select Conda from the list on the top of the screen.

English

Exercise 6.0

From now on, you are expected to write all answers to exercises in a runnable notebook. You can find a template for this notebook here. Download this .ipynb file and use it in VS Code to write down your answers. Add your name and student number to the file.

Nederlands

Opdracht 6.0

Vanaf nu is het de bedoeling dat je al je antwoorden in een Jupyter notebook schrijft. Je kunt het template notebook voor dit hoofdstuk hier vinden. Download dit .ipynb en gebruik het in VS Code om je antwoorden op te slaan. Voeg je naam en studentnummer toe aan het bestand.

Importing a package

If you want to use functions from a package, you first need to import the package. To import a package, at the top of your script/notebook, write import <name>. In the case of NumPy, you should write

import numpy as np

This imports the NumPy package into your script, and lets you refer to it by the name (or alias) np. It is convention to abbreviate NumPy like this. There are hundreds of packages that you can import in Python, and we will introduce some other packages later. It is not uncommon to use ten or more packages in one script, and in that case, you should import all these packages at the top of your script.

A package typically contains many different functions. To use a function from a package, you have to write (in this case) np.<function>. If you don’t use the package name, Python will not understand which function you are referring to, as different packages might have functions with the same name.

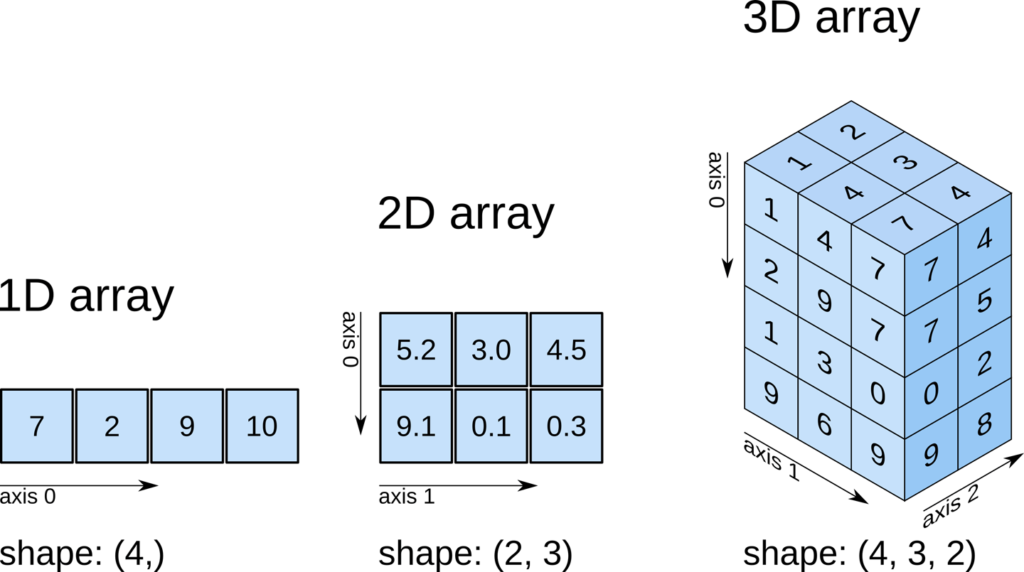
NumPy arrays

Numpy uses objects called arrays to store data. An array is similar to a list, which you have already seen and used. In fact, the easiest way to initialize a NumPy array is using a list. Let’s say that we have a list with numbers numbers = [1, 2, 3], then we can initialize an array containing those numbers.

numbers = [1, 2, 3]
numbers_array = np.array(numbers)

Just as in lists, we can then use indexing and slicing to select numbers in the array

print('List')
print(numbers[0])
print(numbers[1:])
print(numbers[::2])

print('Array')
print(numbers_array[0])
print(numbers_array[1:])
print(numbers_array[::2])

List
1
[2, 3]
[1, 3]
Array
1
[2 3]
[1 3]

Now you might wonder: if arrays are so similar to lists, then why do I need them? There are two answers

1. Arrays are much faster than lists

2. Arrays consume less memory

NumPy contains all kinds of optimized functions to efficiently handle arrays. If you have a computationally heavy piece of code, NumPy arrays are much more efficient than lists. We will demonstrate this later.

NumPy arrays can be easily used to represent vectors. The number of entries of a vector is known as the length or size of the vector. If you have an array defined, you can get this size using the following command.

print(numbers_array.size)

3

This line correctly prints the number of elements in numbers_array. The notation is a bit different from what you have used so far. Thus far, we have used individual variables and we have used functions that can be called as function_name(<arguments>). If we have some variable name followed by .<somevalue> we are asking for an attribute of the object in that variable. We’ll dive deeper into objects later, but what you should understand here is that by getting an attribute, we’re getting some value that is connected to the information stored in the variable.

In the documentation of NumPy you can see that there are several such attributes. Another useful attribute is the shape of an array. You can always find out the shape of your vector by asking for its shape attribute. This shape attribute returns a tuple with the shape of an array, instead of only an integer.

# Print the shape of numbers_array
print(numbers_array.shape)

(3,)

2D (or 3D) arrays

The nice thing about NumPy is that we’re not restricted to 1D vectors as arrays: we can also make 2D, 3D, 4D (etc.) matrices and tensors. To initialize a 2D array from a list, we should create a list of lists, as follows, and call the array function of NumPy

array_2D = np.array([[1, 2],
                     [3, 4]])

print(array_2D)

[[1 2]
 [3 4]]

Similarly, we can create a 3D array from a list of lists of lists. 3D arrays are very useful to represent - for example - medical images. You can think of a 3D array as a cube.

array_3D = np.array([[[1, 2],
                      [3, 4]],
                     [[5, 6],
                      [7, 8]]])

print(array_3D)

[[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]

English

Exercise 6.1

Write code to print the size and shape of array_2D and array_3D.

Nederlands

Opdracht 6.1

Schrijf code die de size en shape van array_2D en array_3D print.

Initializing arrays using lists (of lists (of lists (of lists))) can be tedious. Luckily, NumPy offers functions to directly initialize arrays of various shapes. To fill an array with zeros or ones, you can write

zeros_array = np.zeros((5))
print(zeros_array)
ones_array = np.ones((5))
print(ones_array)

[0. 0. 0. 0. 0.]
[1. 1. 1. 1. 1.]

The argument to these functions is a tuple that describes the shape. If the tuple has two elements, we create a 2D array, if it has three elements a 3D array, etc.

# Initialize a 2D array
print('2D array')
print(np.zeros((2, 2)))
# Initialize a 3D array
print('3D array')
print(np.ones((2, 2, 2)))

2D array
[[0. 0.]
 [0. 0.]]
3D array
[[[1. 1.]
  [1. 1.]]

 [[1. 1.]
  [1. 1.]]]

Because the zeros and ones functions take shape tuples as input, we can also initialize an array based on the shape of another array.

array_3D = np.array([[[1, 2],
                      [3, 4]],
                     [[5, 6],
                      [7, 8]]])

ones_array = np.ones(array_3D.shape)
print(ones_array)

[[[1. 1.]
  [1. 1.]]

 [[1. 1.]
  [1. 1.]]]

A built-in NumPy function that does this is the ones_like (or zeros_like) function. It takes an array as argument and returns a new array with that same shape, but filled with zeros or ones.

ones_array = np.ones_like(array_3D)
print(ones_array)

[[[1 1]
  [1 1]]

 [[1 1]
  [1 1]]]

You can also create arrays with a bit more variation. One commonly used function is the linspace function. This let’s you create an array of evenly spaced values between two numbers. For example, to get 5 values between -1.0 and 1.0, we use

spaced_values = np.linspace(start=-1.0, stop=1.0, num=5)
print(spaced_values)

[-1.  -0.5  0.   0.5  1. ]

Similar to linspace is the arange function. The difference is that the linspace function requires the number of steps while the arange function requires the step size. It’s important to realize that the output of arange does not necessarily include the value of stop. We can see that in the following example. While we use the same start, stop and a step value of 0.5, the value 1.0 is not included because it is not smaller than stop.

spaced_values = np.arange(start=-1.0, stop=1.0, step=0.5)
print(spaced_values)

[-1.  -0.5  0.   0.5]

Random numbers

Another way to initialize arrays is using random numbers. Numpy has a random module that allows you to generate random numbers from several distributions. For example, to generate an array of size (2, 2) with uniformly sampled numbers, you can use

rand_array = np.random.rand(2, 2)
print(rand_array)

[[0.92439953 0.81238608]
 [0.20535585 0.27594122]]

To generate normally distributed random numbers, you can use

randn_array = np.random.randn(2, 2)
print(randn_array)

[[ 1.23733634  0.80177996]
 [ 1.08663424 -1.81928823]]

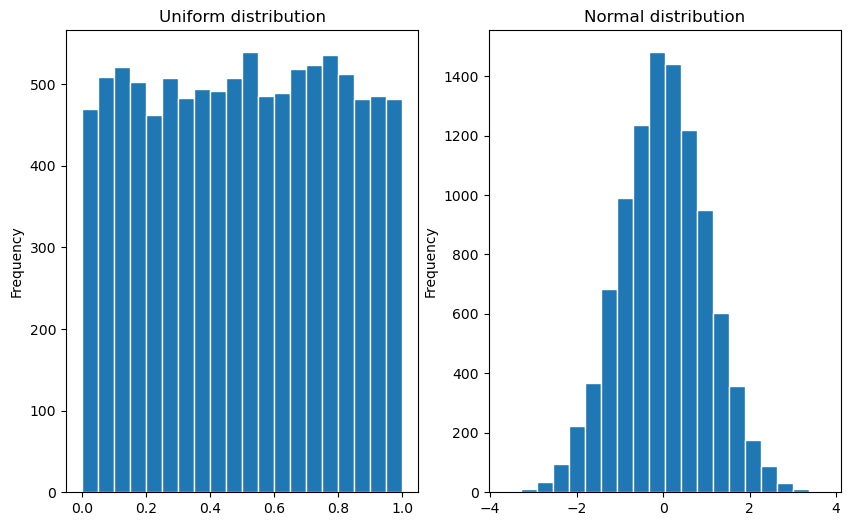
Let’s check what kind of numbers this gives us. You’ll learn all about visualization in the next Chapter, but we will give a sneak preview here. The code below asks NumPy for 10000 random numbers from the uniform and the normal distribution, respectively. Then it plots a histogram of these numbers. As you can see, the distributions are very different. With the normal distribution, we are much more likely to sample numbers close to 0 than further away from 0.

import matplotlib.pyplot as plt

uniform_values = np.random.rand(10000)
normal_values = np.random.randn(10000)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 6))
ax1.hist(uniform_values, bins=20, edgecolor='white');
ax1.set_title('Uniform distribution');
ax1.set_ylabel('Frequency');
ax2.hist(normal_values, bins=20, edgecolor='white');
ax2.set_title('Normal distribution');
ax2.set_ylabel('Frequency');

The rand and randn functions are convenience functions: they are easy to use but don’t provide a lot of options. If you want to control the range of your uniform distribution or the mean and variance of your normal distribution, you should use the uniform and normal functions, respectively. Here, the arguments low, high, loc, scale determine the probability dsitribution. In both cases, size defines the shape of the output.

rand_array = np.random.uniform(low=-5.0, high=5.0, size=(2,2))
print(rand_array)

randn_array = np.random.normal(loc=-10.0, scale=2.0, size=(2,2))

[[-3.26057003  3.79402318]
 [-3.00690893 -2.71545998]]

The randint function draws random integers from a uniform distribution between low and high.

rand_array = np.random.randint(low=0, high=10, size=(2, 2))
print(rand_array)

[[2 2]
 [0 7]]

English

Exercise 6.2

Write a NumPy program to generate a \(5\times 5\) matrix with random integers between 10 and 30.

Nederlands

Opdracht 6.2

Gebruik NumPy om een \(5\times 5\) matrix met willekeurige volledige getallen (integers) tussen 10 en 30 te genereren.

Slicing and indexing

Slicing and indexing in 2D or 3D (or higher-dimensional) NumPy arrays is very useful, but a little more complex than list indexing. By properly indexing and slicing, we can select, change, and remove values. In an array, slicing and indexing is done separately per axis (dimension), and indices are separated by a comma.

Order

When indexing 2D arrays, the first index always corresponds to rows, and the second always to columns.

For example, if we create a \(4\times 4\) array with random numbers and want to select the upper-left quartile, we can do so as follows

square_matrix = np.random.randint(low=0, high=20, size=(4, 4))
print(square_matrix)
print(square_matrix[:2, :2])

[[ 7 18  9  1]
 [18  9  1  9]
 [18 15 13  0]
 [ 4 16  5  9]]
[[ 7 18]
 [18  9]]

Similarly, we can select every second item along each axis

print(square_matrix[1::2, 1::2])

[[ 9  9]
 [16  9]]

As you can see, indexing and slicing is very similar to list indexing and slicing for individual axes, with the only differences that we now have to provide values for each axis. Here, if we want to select all rows/columns in an axis, we just use :

print(square_matrix[0, :])  # Print the first row of square_matrix
print(square_matrix[:, 0])  # Print the first column of square_matrix

[ 7 18  9  1]
[ 7 18 18  4]

Note that the first example is equivalent to square_matrix[0]. When only provided one index (instead of two), Python assumes that the remaining - trailing - axes remain the same.

print(square_matrix[0])

[ 7 18  9  1]

Moreover, we can flip matrices along dimensions by using negative slicing

print(square_matrix[::-1, ::-1])  # Flips the matrix up-down and left-right

[[ 9  5 16  4]
 [ 0 13 15 18]
 [ 9  1  9 18]
 [ 1  9 18  7]]

We cannot just get values using slicing and indexing, but also assign new values. For example, to create a chessboard, we can use indexing to select items in the array, and change their values.

board = np.zeros((8, 8))   # Make an 8 x 8 times array of zeros
board[::2, ::2] = 1        # Set every even element of every even row to 1
board[1::2, 1::2] = 1      # Set every odd element of every odd row to 1
print(board)

[[1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]]

As long as the shape on the left and right of = is the same, we can also change complete rows and columns (or blocks).

rand_matrix_a = np.zeros((5, 5))
rand_matrix_b = np.ones((5, 5))
print('array a')
print(rand_matrix_a)
print('array b')
print(rand_matrix_b)
rand_matrix_a[::2, :] = rand_matrix_b[::2, :]
print('changed a')
print(rand_matrix_a)

array a
[[0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]]
array b
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]
changed a
[[1. 1. 1. 1. 1.]
 [0. 0. 0. 0. 0.]
 [1. 1. 1. 1. 1.]
 [0. 0. 0. 0. 0.]
 [1. 1. 1. 1. 1.]]

English

Exercise 6.3

Use the code below to generate an \(11\times 11\) matrix of integers.

np.random.seed(1337) # Sets the seed of the NumPy random number generator
random_matrix = np.random.randint(0, 100, (11, 11))

The random matrix that you get should look like the example below. Write Python code using indexing to print only

1. the part in blue

2. the part in red

3. the part in yellow

Nederlands

Opdracht 6.3

Gebruik onderstaande code om een \(11\times 11\) matrix van gehele getallen (integers) te genereren.

np.random.seed(1337) # Sets the seed of the NumPy random number generator
random_matrix = np.random.randint(0, 100, (11, 11))

De matrix zou eruit moeten zien zoals hieronder. Schrijf vervolgens Python code met indexing om vanuit deze matrix te printen

1. het blauw gearceerde deel

2. het rood gearceerde deel

3. het geel gearceerde deel

Element-wise operators

NumPy arrays natively support arithmetic operations like +, -, % on two arrays. These are applied in an element-wise fashion: the operator is applied to the pair of items at index 0, index 1, index 2, etc. Here, it’s important to realize that the output is an array with the same shape as the input array. Take a look at the output below to understand what element-wise means.

a = np.array([1, 5, 3, 7]) # Create one array
b = np.array([4, 2, 8, 6]) # Create second array

print(a+b)

[ 5  7 11 13]

print(a/b)

[0.25       2.5        0.375      1.16666667]

print(a//b)

[0 2 0 1]

print(a**b)

[     1     25   6561 117649]

print(a%b)

[1 1 3 1]

What about lists?

We can not perform the operations above with lists, because, e.g., + does something different for lists. If we would treat our 2D matrices as lists of lists instead of NumPy arrays, the code below returns c = [[1, 2, 3], [4, 5, 6], [1, 2, 3], [5, 8, 13]]. I.e., instead of performing addition of individual elements, the lists as a whole are added, and the shape of the list (of lists) changes.

a = [[1, 2, 3],
     [4, 5, 6]]

b = [[1, 2, 3],
     [5, 8, 13]]

c = a + b

We can also apply comparison operators in an element-wise fashion. Just like comparison operators on individual items (Chapter 1), this will return a boolean True or False for each position.

print(a>b)

[False  True False  True]

print(a<b)

[ True False  True False]

print(a==b)

[False False False False]

Moreover, we can use assignment operators +=, -=, *=, etc. directly on arrays

print(a)

[1 5 3 7]

a+=b
print(a)

[ 5  7 11 13]

a-=b
print(a)

[1 5 3 7]

a*=b
print(a)

[ 4 10 24 42]

In addition to these, NumPy has some useful mathematical operators (sqrt, exp, log) etc. that are also applied in element-wise fashion.

print(np.sqrt(a))

[2.         3.16227766 4.89897949 6.4807407 ]

print(np.exp(a))

[5.45981500e+01 2.20264658e+04 2.64891221e+10 1.73927494e+18]

print(np.log(a))

[1.38629436 2.30258509 3.17805383 3.73766962]

print(np.log10(a))

[0.60205999 1.         1.38021124 1.62324929]

Broadcasting

We don’t always need to use element-wise operators with matching pairs of input arrays. For example, if we have some array and we want to multiply all its elements by 4, we don’t have to first make a same-size array of 4’s. Instead, we can simply multiply the full array by 4 through a process called broadcasting. Under the hood, NumPy expands our single number to an array and performs the element-wise multiplication (or addition, subtraction, etc.).

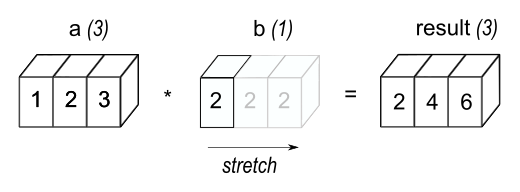
a = np.array([1, 2, 3])
b = 2
result = a * b
print(result)

[2 4 6]

Row/column/array-wise operators

In addition to the element-wise operators, there are operators that work on the full array, or on a single row or column in the array. Consider the min function. As its name implies, it gives the minimal value in an input.

rand_matrix = np.random.randint(low=0, high=10, size=((4, 4)))
print(rand_matrix)
print('The minimum value is {}'.format(np.min(rand_matrix))) # Prints the minimum across *all* entries in the matrix

[[7 9 9 8]
 [3 7 8 8]
 [3 2 5 8]
 [1 3 1 1]]
The minimum value is 1

Sometimes, you might want to get the minimum value per row or per column. In that case, an extra argument should be given for the axis parameter. This is the axis or dimension over which the minimum should be computed. If in this case, we set axis=0, we get the following behavior:

print('The minimum values are {}'.format(np.min(rand_matrix, axis=0)))

The minimum values are [1 2 1 1]

As you can see, the minimum has been computed for each column among the rows, because the rows are axis 0. Conversely, for axis=1, we’d get the following

print('The minimum values are {}'.format(np.min(rand_matrix, axis=1)))

The minimum values are [7 3 2 1]

There are plenty of other functions in NumPy that work in a similar way. You can, for example, use the mean function to compute the average in a row/colum/array, and the std function to compute a standard deviation.

Copy

To copy a NumPy array, you cannot just do new_array = old_array. Because a NumPy array is mutable, any changes made to the old_array will also be applied to new_array. Instead, if you want to make a copy of an array, you should use np.copy(), i.e.

a = np.array([1, 2, 3, 4])
b = np.copy(a)

NaN: Not a number

Not all elements in a NumPy array need to have a value: we can also have arrays with missing values. Imagine for example that we record the weather every day for two weeks and store the result in a NumPy array. However, on two days we forget to record the temperature. We can just fill not a number (NaN) or nan at those indices. This is a placeholder for missing values.

temperatures = np.array([4, 7, 6, 3, 5, 9, np.nan, 4, 10, np.nan, 8, 6, 9, 12])
print(temperatures)

[ 4.  7.  6.  3.  5.  9. nan  4. 10. nan  8.  6.  9. 12.]

We can use the element-wise isnan function to check for NaN values. It will return True for all indices that contain a NaN.

np.isnan(temperatures)

array([False, False, False, False, False, False,  True, False, False,
        True, False, False, False, False])

And if we want to know if there are any NaN values in our array, we can use the any function on this output.

np.isnan(temperatures).any()

True

Using functions like max, sum etc. on an array that contains NaN values will always give you nan as an answer

np.max(temperatures)

nan

np.sum(temperatures)

nan

Luckily, NumPy provides the nan<function> functions that ignore nan values

np.nanmax(temperatures)

12.0

np.nansum(temperatures)

83.0

np.nanmean(temperatures)

6.916666666666667

Advanced indexing

In addition to standard indexing, you can index NumPy arrays in two advanced ways:

1. By providing a list of indices

2. By providing other arrays with boolean values (True and False)

Let’s look at the first option. Here, indices are locations in the array from which we want to get the value. All values at those indices will then be put in a new array.

a = np.array([1, 2, 3, 4, 5])
print(a[[0, 2, -1]])          # Provide a list of indices, here [0, 2, -1]

[1 3 5]

As you can see in the example, we index array a (because we use []), but instead of providing regular indexing rules, we provide a list of indices (which you recognize by []). We ask for the values of a at index 0, 2, and -1 (last element), so we get an array with [1 3 5] back.

Now let’s look at how this works in a 2D array

a = np.random.randint(0, 10, (4, 4))
print(a)
print(a[[0, 2], [1, 3]])

[[8 5 5 3]
 [4 7 7 6]
 [7 2 5 0]
 [4 3 3 3]]
[5 0]

What we have done here, is get the value of a at two locations: a[0, 1] and a[2, 3]. You can think of this as the first argument to our indexing ([0, 2]) providing the row-coordinates, and the second [1, 3] providing the column-coordinates.

In the second advanced indexing option, we provide an array with booleans that has the same shape as the array that we’re indexing. For example, to get the first, third and last element from a, we can do

a = np.array([1, 2, 3, 4, 5])
print(a[[True, True, False, False, True]])

[1 2 5]

This is very useful if you want to filter data according to some criterion. Let’s say that we want to extract from a all values that are larger than 2. You know already that we can use element-wise comparison operators on an array, so we can use > to get a mask that says which indicates for each element in a if it is larger than 2.

mask = a > 2
print(mask)      # This array has the same shape as variable a

[False False  True  True  True]

Now we can use this mask to index a and get all values larger than 2!

print(a[mask])

[3 4 5]

We can also write this shorter

print(a[a>2])

[3 4 5]

The same works if we have a 2D (or higher-dimensional) matrix

a = np.random.randint(0, 10, (4, 4))
print(a[a>2])     # Print all values from the 2D matrix that are larger than 2

[8 5 9 4 8 4 3 8 4 9]

As you see, this returns a 1D array, even though we put in a 2D array. The reason for this is, that when we remove values \(\leq 2\), a is no longer a proper 2D matrix. Hence, NumPy flattens the remaining elements into a 1D vector.

Finally, you can also combine advanced indexing with regular indexing, as long as you choose one method per axes. So, we can for example select all rows from a matrix that match a particular criterion

a = np.random.randint(0, 10, (8, 8))
print('Full matrix')
print(a)
print('Selected rows, every second element')
print(a[np.sum(a, 0)>35, ::2]) # Here we select only those rows whose sum is >35, and in those rows only every second element

Full matrix
[[2 0 2 5 4 9 0 1]
 [2 5 3 4 8 7 5 0]
 [9 6 7 3 8 2 7 3]
 [9 1 6 5 8 5 2 5]
 [2 5 0 8 2 5 0 2]
 [1 6 1 2 9 3 1 4]
 [5 9 4 2 4 4 5 4]
 [5 5 1 2 2 0 3 3]]
Selected rows, every second element
[[2 3 8 5]
 [2 0 2 0]]

Reshaping

If you have an array of a particular shape, you can reshape that array into an array of a different shape, as long the number of items (the size) remains the same. For example, we can reshape a \(2\times 4\) array into a \(4\times 2\) array.

landscape = np.array([[1, 2, 3, 4],
                      [5, 6, 7, 8]])
print(landscape)
portrait = np.reshape(landscape, (4, 2))
print(portrait)

[[1 2 3 4]
 [5 6 7 8]]
[[1 2]
 [3 4]
 [5 6]
 [7 8]]

This is not limited to arrays with the same dimensionality. We can reshape these 2D arrays into 3D arrays as long as the number of items is the same

cube = np.reshape(portrait, (2, 2, 2))
print(cube)

[[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]

Alternatively, we can reshape to a 1D array. This can be done both by the reshape function, or by the flatten method.

bar = np.reshape(cube, (8))
print(bar)

bar_flat = cube.flatten()
print(bar_flat)

[1 2 3 4 5 6 7 8]
[1 2 3 4 5 6 7 8]

Sometimes, you’d want to transpose a matrix by swapping dimensions. In 2D, you can simply achieve this by adding .T. If you have more than two dimensions, you can swap axes using the swapaxes function.

a = np.array([[1, 2],
              [3, 4]])

print(a)
print(a.T)

[[1 2]
 [3 4]]
[[1 3]
 [2 4]]

English

Exercise 6.4

Use NumPy to create a \(7\times 7\) matrix with values ranging from 0 to 48.

Hint: use reshape

Your output should look like this

[[ 0  1  2  3  4  5  6]
 [ 7  8  9 10 11 12 13]
 [14 15 16 17 18 19 20]
 [21 22 23 24 25 26 27]
 [28 29 30 31 32 33 34]
 [35 36 37 38 39 40 41]
 [42 43 44 45 46 47 48]]

Then, use advanced indexing to get a new matrix that contains only rows with four even numbers.

Hint: use the modulo operator %

Your output should look like this

[[ 0  1  2  3  4  5  6]
 [14 15 16 17 18 19 20]
 [28 29 30 31 32 33 34]
 [42 43 44 45 46 47 48]]

Nederlands

Opdracht 6.4

Gebruik NumPy om een \(7\times 7\) matrix met waarden van 0 tot 48 te maken.

Hint: gebruik reshape

Je matrix moet er zo uitzien

[[ 0  1  2  3  4  5  6]
 [ 7  8  9 10 11 12 13]
 [14 15 16 17 18 19 20]
 [21 22 23 24 25 26 27]
 [28 29 30 31 32 33 34]
 [35 36 37 38 39 40 41]
 [42 43 44 45 46 47 48]]

Gebruik vervolgens advanced indexing om een nieuwe matrix te maken die alleen rijen bevat met vier even nummers.

Hint: gebruik de modulus operator %

Je output zou er zo uit moeten zien

[[ 0  1  2  3  4  5  6]
 [14 15 16 17 18 19 20]
 [28 29 30 31 32 33 34]
 [42 43 44 45 46 47 48]]

Combining arrays

If you have two or more 2D arrays, you can join them into a new array using the hstack (horizontal stack) and vstack (vertical stack) functions. For example, we can create two \(2\times 2\) arrays and stack them horizontally or vertically.

a = np.array([[1, 2],
              [3, 4]])
b = np.array([[5, 6],
              [7, 8]])

print(np.hstack((a, b)))

[[1 2 5 6]
 [3 4 7 8]]

print(np.vstack((a, b)))

[[1 2]
 [3 4]
 [5 6]
 [7 8]]

A more general solution (also for higher-dimensional arrays) is to use the concatenate function, which takes an axis as input. This function can be used to mimic either hstack or vstack.

print(np.concatenate((a, b), axis=1)) # Same as hstack

[[1 2 5 6]
 [3 4 7 8]]

print(np.concatenate((a, b), axis=0)) # Same as vstack

[[1 2]
 [3 4]
 [5 6]
 [7 8]]

The tile function builds a grid of repetitions of some input array, like tiling a floor or wall. For example, if we have a 1D array, we can use tile to build a larger array.

element = np.array([1, 2])
tile_result = np.tile(element, (5))
print(tile_result)

[1 2 1 2 1 2 1 2 1 2]

English

Exercise 6.5

Use the tile function to create a chessboard of ones and zeros out of \(2\times 2\) arrays.

Your output should look like this

[[1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]]

Nederlands

Opdracht 6.5

Gebruik de tile functie op \(2\times 2\) arrays om een schaakbord te maken met 0-en (zwart) en 1-en (wit).

De output zou er zo moeten uitzien:

[[1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]
 [1. 0. 1. 0. 1. 0. 1. 0.]
 [0. 1. 0. 1. 0. 1. 0. 1.]]

Loading data

There are several ways to save and load files in NumPy. The most interpretable way is to save and load your matrices as .txt files. For example, if we have a text file numbers.txt whose contents are

4 3 
5 6

we can load these numbers into a NumPy array as follows

import numpy as np

a = np.loadtxt('numbers.txt')
print(a)

and the output would be

[[4. 3.]
 [5. 6.]]

An alternative way is to use the NumPy file format with extension .npy. This lets you store arrays directly from NumPy, one array per file. For example, the following code generates a random array and saves it to a file random.npy.

random_array = np.random.rand(10, 10)
np.save('random', random_array)

We can load this array using np.load as in

random_restored = np.load('random.npy')

The .npy file format only lets you save one array, but you can also store multiple arrays in one file. For this, you need the .npz file format and use it as shown below.

a=np.array([[1, 2, 3], [4, 5, 6]]) # Create an array
b=np.array([1, 2])                 # Create another array
np.savez('multiple.npz', a=a, b=b) # Save both arrays in one file

Now we can again use the load function to load the data, but it doesn’t directly give us back both arrays. Instead, it gives it the object data. We can use its files attribute to check which arrays are stored.

data = np.load('multiple.npz')
print(data.files) # Gives the names of the variables in the npz file
print(data['a'])  # Get the variable with the key 'a'
print(data['b'])  # Get the variable with the key 'b' 
data.close()

['a', 'b']
[[1 2 3]
 [4 5 6]]
[1 2]

In addition to np.savez there is also np.savez_compressed which is used the same way, but writes smaller files. This can be useful when you have large arrays.

Vectorization

Because NumPy operates on arrays of elements instead of individual elements, it is very fast. We can verify this using timeit magic. Let’s reuse the dot_product function that you created in Chapter 4. The function loops over the elements in two vectors, multiplies them, and then sums all the products.

# Dot product 
import numpy as np

def dot_product(a, b):
    dot = 0
    for v_a, v_b in zip(a, b):
        dot += v_a * v_b
    return dot

In the cell below, we use %timeit (as explained in Chapter 5) to run this function 100 times on a vector of 1000 elements.

a = np.random.randint(0, 1000, 1000) # Make a random array
b = np.random.randint(0, 1000, 1000) # Make another random array

%timeit -n 100 dot_product(a, b)     # Use our for loop

225 µs ± 2.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

The output tells you how lung it takes on average to run this function with this input.

NumPy has a dot function that should give you the exact same result. In the cell below, we again use %timeit on that function, with the same input and number of runs.

%timeit -n 100 np.dot(a, b)          # Use the standard NumPy function

2.73 µs ± 1.99 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

As you can see, this is (depending on your computer), at least 20 times faster!

Speed

for-loops are always slower than properly vectorized functions. When possible, use a NumPy function instead of a for-loop when operating on arrays.

Linear algebra

We will not go into too much detail here, but it’s good to be aware that NumPy provides the linalg module that contains many of the functions that you will need for linear algebra. The documentation provides a list of all functions.

English

Exercise 6.6

Compare runtimes for the following functions that can be used to compute the sum of an array

• With a for loop

• Using a recursive function like the one you made in Exercise 4.5.

• Using the sum function in NumPy.

Base your solution on the script above. Before you run the code, consider which method you think is fastest, and which slowest. How much faster is the fastest method than the slowest method? How does the size of the input vector affect the runtime and speed-up?

# Use a for loop to compute the sum of a 1D NumPy array
def loop_sum(a: np.array):
    total = 0
    for v_a in a:
        total += v_a
    return total

# Use recursion to compute the sum of a 1D NumPy array
def recurse_sum(a: np.array):
    if a.size == 1:
        return a[0]
    else:
        return a[0] + recurse_sum(a[1:])
    
# Use NumPy's sum function to sum a 1D NumPy array
def numpy_sum(a: np.array):
    return np.sum(a)

Nederlands

Opdracht 6.6

Vergelijk de runtime van drie manieren op de som van een array te bepalen:

• Met een for loop.

• Met een recursieve functie zoals je die hebt bepaald in Opdracht 4.5.

• Met de sum functie in NumPy.

Baseer je script op het script hierboven. Bedenk vooraf welke functie sneller zal zijn. Functies zijn hieronder gegeven. Hoeveel sneller is de snelste functie ten opzichte van de andere functies? In hoeverre heeft de lengte van de input array invloed op de tijd die het duurt om de functie uit te voeren?

# Use a for loop to compute the sum of a 1D NumPy array
def loop_sum(a: np.array):
    total = 0
    for v_a in a:
        total += v_a
    return total

# Use recursion to compute the sum of a 1D NumPy array
def recurse_sum(a: np.array):
    if a.size == 1:
        return a[0]
    else:
        return a[0] + recurse_sum(a[1:])
    
# Use NumPy's sum function to sum a 1D NumPy array
def numpy_sum(a: np.array):
    return np.sum(a)

NumPy functions and methods

For many operations, NumPy offers functions. These are similar to the functions you have seen in Chapter 4. They take an input and return an output. For example - as you have seen - we can sum all elements in an array using the sum() function.

some_array = np.random.rand(10)
print(np.sum(some_array))

5.834175759227194

However, for most functions that take an array as argument, you can also use a method instead. This is a function that directly operates on the array, and is called by adding . and the method name after the name of your NumPy variable. So, to compute the sum of some_array, we do

print(some_array.sum())

5.834175759227194

Some other examples are

print('min')
# Function
print('Function {}'.format(np.min(some_array)))
# Method
print('Method {}'.format(some_array.min()))

min
Function 0.2458941386430764
Method 0.2458941386430764

print('sum')
# Function
print('Function {}'.format(np.sum(some_array)))
# Method
print('Method {}'.format(some_array.sum()))

sum
Function 5.834175759227194
Method 5.834175759227194

print('mean')
# Function
print('Function {}'.format(np.mean(some_array)))
# Method
print('Method {}'.format(some_array.mean()))

mean
Function 0.5834175759227194
Method 0.5834175759227194

print('reshape')
# Function
print('Function {}'.format(np.reshape(some_array, (5, 2))))
# Method
print('Method {}'.format(some_array.reshape(5, 2)))

reshape
Function [[0.63120072 0.4924672 ]
 [0.24589414 0.96001143]
 [0.30490878 0.74468667]
 [0.69458278 0.59666093]
 [0.50352123 0.66024187]]
Method [[0.63120072 0.4924672 ]
 [0.24589414 0.96001143]
 [0.30490878 0.74468667]
 [0.69458278 0.59666093]
 [0.50352123 0.66024187]]

You can find a full overview of all methods in the NumPy documentation. While methods can in principle be a tiny bit faster than functions, they are equivalent in many cases, and it is mostly readability of your code that defines if you should use a method or function. However, there are some cases where the function returns a copy of the array, while the method operates in-place and there thus is a difference. An example is sort.

unsorted_array = np.random.randint(0, 10, (10))
print(unsorted_array)

[9 0 5 0 2 8 0 8 4 0]

sorted_array = np.sort(unsorted_array) # Use the sort function
print('Sorted array after sorting: {}'.format(sorted_array))
print('Unsorted array after sorting: {}'.format(unsorted_array))

Sorted array after sorting: [0 0 0 0 2 4 5 8 8 9]
Unsorted array after sorting: [9 0 5 0 2 8 0 8 4 0]

As you can see, when using the function, the unsorted_array variable remains unchanged. Instead, if we use the method as below, we change the array in place and we no longer have our unsorted array.

unsorted_array.sort()
print('Unsorted array after sorting: {}'.format(unsorted_array))

Unsorted array after sorting: [0 0 0 0 2 4 5 8 8 9]

English

Exercise 6.7

Download the .npy file grades.npy from here. This file contains (fictional) grades for an exam and resit of a class of students. The first column contains the grades for the exam, the second column grades for the resit. Load the file using NumPy and write code to answer the following questions:

1. How many students are in the class?

2. How many students passed the exam the first time (grade \(\geq 5.5\))?

3. What was the average grade of students that passed the exam the first time?

4. Not all students that failed the exam, also took the resit. How many students didn’t?

   Hint: Use isnan

5. Some students passed the exam the first time, but still took the resit. The highest grade counts. What is the average final grade of all students that passed the course? Hint: Use nanmax

Nederlands

Opdracht 6.7

Download het .npy bestand grades.npy van hier. Dit bestand bevat (fictieve) cijfers van een klas studenten voor een tentamen en herkansing. De eerste kolom bevat de cijfers voor het examen, de tweede kolom voor de herkansing. Laad het bestand met NumPy en schrijf code om de volgende vragen te beantwoorden:

1. Hoeveel studenten zitten er in de klas?

2. Hoeveel studenten hebben het tentamen de eerste keer gehaald (cijfer \(\geq 5.5\))?

3. Wat was het gemiddelde cijfer van studenten die het tentamen de eerste keer haalden.

4. Niet alle studenten die het tentamen niet haalden, hebben de herkansing gedaan. Hoeveel studenten hebben de herkansing laten schieten?

   Hint: Gebruik isnan

5. Sommige studenten haalden het eerste tentamen, maar deden alsnog de herkansing. Het hoogste cijfer telt. Wat is het gemiddelde eindcijfer van alle studenten die het vak gehaald hebben? Hint: Gebruik nanmax

English

Exercise 6.8

A magic square is a square matrix whose rows, columns, and two diagonals all sup um to the same value. This value is called the magic value. An example of a magic square is shown below

In this exercise, you will write a function check_magic_square that uses NumPy to check whether an input array is a magic square or not. If the input array is a magic square, the function should return True and the magic vale. If it is not a magic square, the function should return False and the reason why it is not.

Some guidelines/rules:

1. This is a function, so use what you learned in Chapter 4.

2. Use if/else to check if all conditions for a magic square are met.

3. Try to use NumPy and avoid the use of for loops.

To check whether your function is working properly, you can apply it on the arrays in an npz file that you can download here. Load this npz file and apply your function to each individual array.

Nederlands

Opdracht 6.8

Een magisch vierkant of tovervierkant is een vierkante matrix waarvan de rijen, kolommen, en diagonalen allemaal optellen tot hetzelfde getal, het magische getal. Een voorbeeld van zo’n tovervierkant met magisch getal 15 is te zien op de afbeelding hieronder

In deze opdracht ga je zelf een functie check_magic_square schrijven die een NumPy array als input neemt en met behulp van NumPy bepaalt of de array een tovervierkant is of niet. Zoja, dan moet de functie. True teruggeven en het magisch getal. Zo niet, dan moet de functie False teruggeven en de reden waarom de input geen tovervierkant is.

Een paar hints en regels:

1. Je moet een functie schrijven, dus gebruik wat je geleerd hebt in Hoofdstuk 4.

2. Gebruik if/else om te controleren of aan alle voorwaarden voor een tovervierkant voldaan is.

3. Probeer zoveel mogelijk gebruik te maken van NumPy en vermijd for loops.

Om te kijken of je functie goed werkt, kun je gebruik maken van de arrays die we in een npz bestand hebben geplaatst dat je hier kunt downloaden. Laad dit npz bestand in en pas je functie toe op de arrays in het bestand.

There’s more

NumPy is a large package, and we have here only given an introduction to all functions in NumPy. As you program more, you will get to know more and more functions. Cheatsheets like the one here can also help you get a quick overview of all functions in NumPy.