Functions#
Learning goals
After finishing this chapter, you are expected to
define a function in Python
understand the concept of scope, local and global variables
create a function with one or more input arguments and one or more output arguments
understand what recursion is and how to use it
By now you can write and run a Python script, you can write conditional statements using if, elif and else, and you can write for and while loops. You can ask the user for input to dynamically change what happens in a script. You’ve seen that with these building blocks, you can already solve some problems and write small programs. However, if you write scripts with only these building blocks, they can become quite lengthy. Most programming languages use functions. In Python, functions are everywhere. In fact, you have already used functions: for example, the print() function outputs something to the screen. We call this function with some input, and it writes this input to the terminal.
print('Hello')
print('Goodbye')
Hello
Goodbye
Other functions that you have used so far are len() and input(). You can think of a function as a mini-program that runs within another program or within another function. The main program calls the mini-program and sends information that the mini-program will need as it runs. When the function completes all of its actions, it may send some data back to the main program that has called it. The primary purpose of a function is to allow you to reuse the code within it whenever you need it, using different inputs if required. When you use functions, you are extending your Python vocabulary. This lets you express the solution to your problem in a clearer and more succinct way. Functions can be used many times within one script. For example, when training a neural network, you call the same functions thousands or millions of times.
A basic function#
Let’s start by defining a very simple function. The header of a function always starts with the keyword def, followed by the name of the function, parentheses, and a colon :. The body of a function contains the actual Python lines that will be executed. The body is a block of code with indentation, just like the statement if you use if or for. We can define a function that simply writes ‘Hello world’ to the terminal.
def hello_world(): # This is the header of the function
print('Hello world') # This is the body of the function
Defining a function does not lead to any output. The function is simply there, but not used. To use the function we have to call it, like this:
hello_world() # Call the hello_world function
Hello world
By calling the function, its body gets executed. In this case, the body of the function only contains a call to the built-in print function. This also shows that you can call functions from within other functions.
The use of ( and )
Any time you call a function (i.e., use it), you have to use a ( and a ). Note that this is different from indexing a list, tuple, dictionary, for which you use [ and ].
Where do you put a function?#
You’ve learned to write Python scripts as .py files. You can simply add functions to your script so that they can be used in that script. For example, the following would be a valid .py file that you can run in VS Code. Try it out!
def hello_world(): # This is the header of the function
print('Hello world') # This is the body of the function
hello_world() # Call the hello_world function
Hello world
It is important that you define your functions before you use them. Otherwise, the interpreter does not understand which function you’re referring to. So, the following will not work:
hello_world() # We're trying to call the hello_world function, but it has not been defined
def hello_world():
print('Hello world')
Function naming conventions
In Python, naming conventions for functions are the same as for variables. You should use lowercase letters, and separate words with an underscore, as in the hello_world() example above. Since functions represent actions, it’s best practice to start your function names with a verb to make your code more readable.
Functions with arguments#
Things get more interesting if our function does not do exactly the same whenever it is called, but changes what it does depending on the input that we provide. For example, we can write a function that takes two numbers and decides which of the two numbers is smallest. For this, we use things that you have already learned: e.g, if, elif, else, string formatting. You can see that the body of the function is just a mini-program whose variables are defined in the header of the function.
def find_smallest(number_a, number_b): # The header of the function with two parameters
if number_a < number_b:
print('{} is the smallest number'.format(number_a))
elif number_b < number_a:
print('{} is the smallest number'.format(number_b))
else:
print('Both numbers are equal')
This function has two parameters: number_a and number_b. These parameters are used in the body of the function, in this case in an if-statement with comparison operators <. Now, if we want to use this function, we have to call it using arguments, i.e., values for the parameters, as follows:
find_smallest(number_a = 45, number_b = 23) # Call the function using two arguments
23 is the smallest number
In general, you can create a function with any type of variable. Arguments can also be lists, tuples, dictionaries, etc. However, when you call a function, there is a chance that your type is not compatible with the type that the function was intended for. In that case, Python will throw an exception. You can help others reading your code by type hinting: indicating in your function header which type is expected. For the find_smallest() function this might look like the following.
def find_smallest(number_a: int, number_b: int): # We have here added types to number_a and number_b
if number_a < number_b:
print('{} is the smallest number'.format(number_a))
elif number_b < number_a:
print('{} is the smallest number'.format(number_b))
else:
print('Both numbers are equal')
Note that type hinting is a form of documentation: it doesn’t change how Python treats your code, but it makes your code more reusable, just like placing comments with # and using descriptive names for variables and functions.
Exercise 4.1
Consider Exercise 3.3 about banking. Adapt that script into a function called evaluate_customer that takes in a customers age (as int) and annual income (as int) as parameters and prints the required answer. Test your code by calling the function as follows
def evaluate_customer(age: int, annual_income: int):
## The body of the function goes here
evaluate_customer(40, 11000)
evaluate_customer(18, 25000)
evaluate_customer(30, 40000)
evaluate_customer(15, 5000)
Exercise 4.2
Write a function print_code that takes a ‘code’ as input and uses that code to print characters to the command line. A code is a string that describes which characters should be printed. Each code consists of pairs of characters and counts. The maximum count is 9. For example,
when called as
print_code('6+')the function should print++++++when called as
print_code('2+4*5+')the function should print++****+++++when called as
print_code('2*4+6*')the function should print**++++******,when called as
print_code('9a4b3c')the function should printaaaaaaaaabbbbccc
To help you get started, here is a layout for your function. You have to change the commented lines in order to make the function work.
def print_code(code):
output = ''
for start_ind in range(0, len(code), 2):
fragment = code[start_ind:start_ind+2]
#### based on the fragment, extend the output string
#### print the output string
Finish this function and verify that your function works using the examples shown above.
The list below contains multiple codes. Write a script that loops over this list and prints each code. Note that these codes contain spaces. These are treated like characters by Python.
full_code = ['9 5 6+7 6+', '9 3 9+1+3 9+1+', '9 1 9+4+1 9+4+', '9 9+9+9+2+', '9 9+9+9+2+', '9 9+9+9+2+', '9 1 9+9+9+', '9 3 9+9+5+', '9 5 9+9+1+', '9 7 9+6+', '9 9 9+2+', '9 9 2 7+', '9 9 4 3+', '0+']
Return#
The hello_world, find_smallest, and print_code functions only print a result, but do not return anything. In many cases, you will want to use a function to give you some output value that you can use in your script, instead of only writing the answer to the terminal. In Python, we use the keyword return to send the result of the function call back to wherever the function was called from. Let’s make a very basic function that adds two numbers and returns the result.
def add_numbers(number_a, number_b):
return number_a + number_b
sum_of_numbers = add_numbers(number_a = 34, number_b = 21) # The result of the function call is stored in sum_of_numbers
print('The sum is {}'.format(sum_of_numbers)) # We can print the value of sum_of_numbers (or use it for something else)
The sum is 55
When we call this function, the sum of both numbers is computed and immediately returned. It then takes the place of add_numbers(number_a = 34, number_b = 21), which means that the line now says
sum_of_numbers = 55
and that the result is directly assigned to the variable sum_of_numbers.
A function can return more than one value. Values to be returned should be separated by a comma, and the output of the function should be assigned to the same number of variables. For example, we can write a function that returns two values: the sum and the product of its inputs.
def compute_sum_and_product(number_a, number_b):
sum_of_numbers = number_a + number_b
product_of_numbers = number_a * number_b
return sum_of_numbers, product_of_numbers # Return two values, separated by ,
summed, multiplied = compute_sum_and_product(4, 8) # Assign result of the function call to two variables
print(summed)
print(multiplied)
12
32
Returning pass
In some cases - when you’re coding - it might be convenient not to return anything at all but to already type the header of a function. To make sure that your code runs, each function must return something, but what do you return if the function isn’t finished? A solution is to return pass, which can be used as a placeholder for future code. Note that this can also be used in control structures like if, else, and loops.
def unfinished_function():
return pass
Optional arguments#
Python differentiates between required and optional arguments. Required arguments should always be provided to the function. If they are not provided, Python throws an error. Consider our add_numbers() function above: it has exactly two parameters: number_a and number_b. If fewer or more arguments are provided, Python throws an error:
add_numbers(number_a = 3)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
/var/folders/07/x0gf6dj176dfjvrn357t5p6h0000gn/T/ipykernel_34291/2140094660.py in <module>
----> 1 add_numbers(number_a = 3)
TypeError: add_numbers() missing 1 required positional argument: 'number_b'
add_numbers(number_a = 3, number_b = 4, 5)
File "/var/folders/07/x0gf6dj176dfjvrn357t5p6h0000gn/T/ipykernel_34291/3779491282.py", line 1
add_numbers(number_a = 3, number_b = 4, 5)
^
SyntaxError: positional argument follows keyword argument
In this example,number_a and number_b are both required arguments. Because of this, we actually don’t have to specify which parameter we’re assigning the argument to when we call the function. We can call the function with or without parameter names.
add_numbers(number_a = 14, number_b = 75) == add_numbers(14, 75)
True
A way to make your code more flexible is to use optional arguments. If these are not provided, the function still runs. This is because we provide default parameter values: if the user does not provide other values, these are used. Consider the following variant on our function, which assumes that number_b = 37 if not provided.
def add_numbers_optional(number_a, number_b = 37):
return number_a + number_b
print(add_numbers_optional(34, 52))
print(add_numbers_optional(12))
86
49
To prevent ambiguity about the correspondence between parameters and arguments, it’s good to use parameter names when calling a function, like this:
print(add_numbers_optional(number_a = 34, number_b = 52))
86
It is important that if you provide default values for arguments, that this should be done for the last parameter, second-to-last, etc. The parameter list of your function cannot have a required argument after an optional one.
def add_numbers_optional(number_a = 37, number_b):
return number_a + number_b
print(add_numbers_optional(number_a = 34, number_b = 52))
File "/var/folders/07/x0gf6dj176dfjvrn357t5p6h0000gn/T/ipykernel_34291/1073581284.py", line 1
def add_numbers_optional(number_a = 37, number_b):
^
SyntaxError: non-default argument follows default argument
Exercise 4.3
A common operation in linear algebra is computing the dot product between two vectors. The dot product of two vectors \(\mathbf{a}=[a_1, a_2, \ldots, a_n]\) and \(\mathbf{b}=[b_1, b_2, \ldots, b_n]\) is defined as
Write a function that takes two vectors \(\mathbf{a}\) and \(\mathbf{b}\) as lists as input and returns their dot product as a floating point number. The dot product can only be computed if the length of \(\mathbf{a}\) and \(\mathbf{b}\) is the same. Let your function check that this is the case, and if not, print a message for the user and return -1. Call your function dot_product() and use the code below to test it
vector_a = [3, 5, 9]
vector_b = [3.2, 6, -5]
print(dot_product(vector_a, vector_b))
vector_a = [3, 5, 9, 4]
vector_b = [3.2, 6, -5]
print(dot_product(vector_a, vector_b))
Scope#
Each variable in Python has a scope. This influences the way that variables are looked up in your code. So far, we have worked with global variables. These are variables that can be accessed anywhere in the code. Setting the value of the variable in a for or while loop or in an if-statement changes the value everywhere. When working with functions, we have to consider the scope of a variable. This means that if a variable is defined in a function, it cannot be accessed outside of that function.
Take a look at the following example. We have defined a simple function add_y that adds some number to its input. The function works well and we can verify this with the first print statement. The number that is added is defined in a local variable y. This variable only exists within the function add_y. If we want to print the value at the global level with print(y) Python gives a NameError: it cannot find the variable y because it does not exist globally.
def add_y(x):
y = 8
return x + y
print(add_y(10))
print(y)
18
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
/var/folders/07/x0gf6dj176dfjvrn357t5p6h0000gn/T/ipykernel_34291/1922670122.py in <module>
4
5 print(add_y(10))
----> 6 print(y)
NameError: name 'y' is not defined
This also works the other way: if we define a global variable y, the function will ignore its value and just use the local variable y as long as it’s defined. Here, we see that although our global variable y is 4 and remains 4, the value of y in the function is 5.
y = 4
def add_y(x):
y = 8
return x + y
print(add_y(10))
print(y)
18
4
However, if there is no local variable y in the function, the global variable y will be used instead, as below.
y = 4
def add_y(x):
return x + y
print(add_y(10))
print(y)
14
4
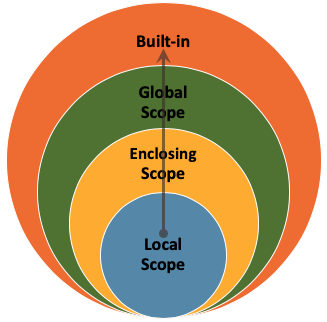
There is a particular priority system that Python uses to look up the value of a variable, the LEGB-rule. This stands for local, enclosed, global, built-in.
Local: these are variables that are defined only in a function.
Enclosed: an (inner) function can be defined inside another (outer) function. The inner function is able to access the variables of the outer function, but not the other way around.
Global: global variables at the level of your script.
Some variable names are
built-inand are always accessible from everywhere. These are the keywords that you have seen before, i.e.:
If the interpreter looks for the value of a variable, it does so bottom-up, starting at the local level. The figures below nicely visualize this process. Here, x is defined within the inner function, so that is the value that is used at that point. If x was not defined in the inner function, then x in the outer function would be used. If that variable had not been defined, a global variable x would be used. And if that didn’t work, the interpreter would look for a built-in variable x (which does not exist).
Recursive functions#
We can call functions from anywhere in a script, as long as it has been defined. Moreover, in Python (and in many other languages) there is no reason why a function cannot be called from within itself. This is called a recursive function. Recursion is a concept that can be difficult to understand. The core idea is that you repeatedly call the same function from within itself. This means that the operations that you’re applying should be very similar each time the function is called. A well-known example is the factorial \(n!=n \times n-1 \times n-2 \times \cdots \times 2 \times 1\). We can implement this in a recursive function as
def factorial(n): # 1
if n > 1: # 2
return n * factorial(n-1) # 3
else: # 4
return 1 # 5
factorial(3)
6
Exercise 4.4
In the factorial() function above, we have added line numbers in comments. Look at the code and see if you can figure out in which order the lines are executed if you call factorial(3).
To write a proper recursive function, you need an if and else expression, where each one corresponds to one of the two scenarions:
A ‘base’ condition. This is the point at which the recursion stops and moves back ‘up’.
A change that is applied so that your process comes closer to reaching the base condition.
In the example above, the base condition is \(n=1\), and the change that is applied is \(n-1\). If there is no base condition or no change, your function will just run indefinitely, like a while loop without a stopping condition.
Exercise 4.5
Write a function sum_recursion to calculate the sum of a list of numbers using recursion.
Hint: In your base condition, there is only one item left in the list.
Test your function using the following code.
def sum_recursion(numbers):
# Your function body
numbers_list = [2, 3, 1, 6, 7, 8, 4]
summed_list = sum_recursion(numbers_list)
print('The sum of {} is {}'.format(numbers_list, summed_list))
Opdracht 4.5
Schrijf een functie sum_recursion die met behulp van recursie (zoals in de factorial functie gebruikt wordt) de som van een list met getallen bepaalt. Dus, stel dat we een lijst getallen [2, 3, 1, 6, 7, 8, 4] hebben, dan moet de functie 31 als antwoord teruggegeven.
Zorg ervoor dat de functie een if en een else statement bevat. Hier staat een opzetje van de functie en code om je functie te testen.
def sum_recursion(numbers):
if len(numbers) == 1:
return numbers[0]
else:
# Your code
numbers_list = [2, 3, 1, 6, 7, 8, 4]
summed_list = sum_recursion(numbers_list)
print('The sum of {} is {}'.format(numbers_list, summed_list))
Built-in functions#
You don’t have to define each function yourself: Python has a number of built-in functions that are available in any Python distribution. Useful functions include the len, print and input functions that you have already used. In addition to the functions that you can write yourself, Python has a number of built-in functions. These are functions that are always available if you program in Python. Examples are print(). A complete list of built-in functions is available here. Take a look, you’ll likely recognize some of them. We have previously used the round() and range() functions, and it’s clear what - for example - the abs() does. Likewise, you have used the type() function to find out what the type of a variable is.
Exercise 4.6
There are many cases in programming where we need to sort something, usually in ascending order (low to high), sometimes in descending order (high to low). There are also many different sorting algorithms, some faster than others, some more complex. The animation below visualizes eight popular sorting algorithms. The length of the bars indicated their value, and as you can see, each algorithm tries to sort the values from low to high (in ascending order).
In this exercise, you will implement bubble sort. Bubble sort is not the fastest algorithm (as you can see in the animation), but it is (relatively) easy to understand. Let’s say that we have a list of numbers that we want to sort. The animation below visualizes bubble sort for a short list.
Bubble sort does the following:
Check if the first element in the list is greater than the next element in the list.
If it is greater, swap the two elements. Otherwise, repeat step 1 for the next element in the list.
Repeat steps 1 and 2 until you reach the end of the list.
Check if all elements are sorted:
If not, repeat the process in step 1 to 3. However, you can now ignore the last element because you know it has the highest value and is in the right place. The next iteration you can ignore the last two elements, etc.
If yes, the final output is a sorted array.
Your task in this exercise is to implement a bubble sort function. Use the provided code below and fill in the missing parts.
Hint Use a while loop to check whether the list is sorted. You can use the provided check_sorted function.
import numpy as np
def check_sorted(numbers):
for i in range(len(numbers)-1):
if numbers[i] >= numbers[i+1]:
return False
return True
def bubble_sort(numbers):
# Your code goes here
numbers = list(np.random.permutation(100))
print(numbers)
print('The list of numbers {} sorted'.format('is' if check_sorted(numbers) else 'is not'))
sorted_numbers = bubble_sort(numbers)
print(sorted_numbers)
print('The list of numbers {} sorted'.format('is' if check_sorted(sorted_numbers) else 'is not'))
Opdracht 4.6
Er bestaan veel verschillende manieren om een lijst te segmenteren. De animatie hieronder laat een paar van die algoritmes zien. Zoals je kunt zien, zijn sommige algoritmes sneller dan andere algoritmes.
In deze opdracht ga je zelf een sorteeralgoritme implementeren. Het algoritme dat je gaat implementeren is bubble sort. Bubble sort is niet zo snel, maar wel eenvoudig om te begrijpen. De animate hieronder visualiseer het principe van bubble sort.
Bubble sort werkt als volgt voor een lijst getallen die ik oplopende volgorde wordt gesorteerd:
Loop door de gehele lijst getallen heen. Als er twee buurelementen zijn in de lijst die niet op de goede volgorde staan (dus de eerste is hoger dan de tweede), draai je die om. Als je op deze manier één keer door de hele lijst bent gestapt weet je dat de hoogste waarde zich in ieder geval geheel op het einde bevindt.
Controleer of de lijst goed gesorteerd is. Als dat het geval is geef je de rij terug als oplossing.
Als de rij niet gesorteerd is loop je nog een keer door de hele rij heen, maar negeer je het laatste element: je weet immmers dat dat de hoogste waarde is.
Dit process herhaal je tot de hele lijst goed gesorteerd is. Telkens negeer je een extra element aan het einde van de lijst, want na \(n\) stappen weet je dat de \(n\) elementen op het einde van de lijst wel goed gesorteerd zijn.
Het doel van deze opdracht is een eigen implementatie te maken. In onderstaande code moet je de missende regels toevoegen. We raden aan om een while loop te gebruiken om telkens te checken of de rij gesorteerd is. Om te kijken of de rij gesorteerd is, kun je de check_sorted functie gebruiken.
import numpy as np
def check_sorted(numbers):
for i in range(len(numbers)-1):
if numbers[i] >= numbers[i+1]:
return False
return True
def bubble_sort(numbers):
# Your code goes here
numbers = list(np.random.permutation(100))
print(numbers)
print('The list of numbers {} sorted'.format('is' if check_sorted(numbers) else 'is not'))
sorted_numbers = bubble_sort(numbers)
print(sorted_numbers)
print('The list of numbers {} sorted'.format('is' if check_sorted(sorted_numbers) else 'is not'))
Exercise 4.7
Write a Python function that takes a number \(n\) as a parameter and returns all prime numbers up to \(n\) as a list. Tip: you can consider this algorithm to make your function efficient. Name your function all_primes() and use the following code to test it
def all_primes(n):
# The body of your function goes here
n = #
primes = all_primes(n)
print(primes)
Opdracht 4.7
Schrijf een Python functie die alle priemgetallen tot het getal \(n\) in een lijst terug geeft (returnt). Dus bijvoorbeeld, voor n=8 moet de functie [2, 3, 5, 7] teruggeven. Je kunt hiervoor de Zeef van Eratosthenes gebruiken. Dit is een bekend algoritme waarbij je telkens het volgende doet
Maak een gesorteerde lijst van alle getallen van 2 tot \(n\).
Kies het kleinste getal uit de lijst.
Streep alle veelvouden van het gekozen getal door (maar niet het getal zelf).
Kies het volgende getal uit de lijst en ga verder met stap 3.
.
Noem je functie all_primes() en gebruik de code hieronder om je functie te testen.
def all_primes(n):
# The body of your function goes here
n = #
primes = all_primes(n)
print(primes)