Tutorial 4#
March 11, 2025#
In the first tutorials, you have trained and evaluated supervised models for image classification and segmentation. In this tutorial, we will take a closer look at generative models. We will again build on PyTorch, MONAI and Weights & Biases. Let’s first make sure that you have access to MONAI. As always, if you’re running this on Colab, make sure that you select a runtime with GPU.
import torch
import random
# Check whether we're using a GPU
if torch.cuda.is_available():
n_gpus = torch.cuda.device_count() # Total number of GPUs
gpu_idx = random.randint(0, n_gpus - 1) # Random GPU index
device = torch.device(f'cuda:{gpu_idx}')
print('Using GPU: {}'.format(device))
else:
device = torch.device('cpu')
print('GPU not found. Using CPU.')
Pretrained models
You can download some pre-trained generator models for the GAN training exercises from this link, but of course it’s much more interesting to train them yourself. Use
path = 'saved_models/CNN_GAN/Epoch_50.pt'
checkpoint = torch.load(path)
epoch = checkpoint['epoch']
generator.load_state_dict(checkpoint['generator'])
discriminator.load_state_dict(checkpoint['discriminator'])
optimizer_gen.load_state_dict(checkpoint['optimizer_gen'])
optimizer_dis.load_state_dict(checkpoint['optimizer_dis'])
to load the model (see also: this link).
You can monitor the GPU activity using [watch] nvidia-smi in a terminal. Ultimately you can even identify the ID of the jobs ran by your classmates to know who is using what.
Consider dialogue before disconnecting them from the network using illegal ways.
1D generative adversarial network (GAN)#
We define a GAN consisting of two neural networks that play a game:
The discriminator will learn to distinguish real and fake samples in \(z\)
The generator will generate fake samples in \(z\) that the discriminator cannot discriminate
In the lecture, you have seen this simple 1D problem. We assume that there is a data set of real samples that are drawn from a normal distribution (the black dotted line below). These samples are in the sample domain and are called \(x\). The generator network does not know anything about the distribution of the real samples in the sample domain, but will try to converge to a function that maps random noise \(z\) to samples that seem to come from the real sample distribution (the green line below). The discriminator network is the adversary of the generator and it tries to distinguish real samples from fake samples. It’s predictions on \(x\) are shown with a blue curve in the figure.

First, let’s set up the data for this toy problem. We define the mean value of the normal distribution from which real samples will be drawn in the sample domain \(x\). In addition, we define the dimensionality of the normal distribution \(z\) from which noise samples to the generator will be drawn, i.e. the latent space. For now, we can assume a 1-dimensional noise distribution.
# Determines the distribution of the real samples N(real_mean, 1)
real_mean = 8
# Determines the dimensionality of the latent space
latent_dim = 1
The cell below defines the generator and discriminator networks. These are very simple networks that map scalars to scalars through a hidden layer. In this case, the networks are actually identical.
import torch
import torch.nn as nn
# The discriminator will directly classify the input value
class Discriminator_1D(nn.Module):
def __init__(self):
super(Discriminator_1D, self).__init__()
self.layers = nn.Sequential(nn.Linear(in_features=1, out_features=32),
nn.LeakyReLU(),
nn.Linear(in_features=32, out_features=1))
def forward(self, x):
return self.layers(x)
# The generator will transform a single input value
class Generator_1D(nn.Module):
def __init__(self):
super(Generator_1D, self).__init__()
self.layers = nn.Sequential(nn.Linear(in_features=1, out_features=32),
nn.LeakyReLU(),
nn.Linear(in_features=32, out_features=1))
def forward(self, x):
return self.layers(x)
Now, we will define the training functions for both networks. Consider what is actually happening in a GAN and how the inputs and outputs are connected. The overall objective function of our system is as follows
\(V^{(D)}(D,G)=\underset{x\sim p_{data}}{\mathbb{E}} [\log{D(x)}]+\underset{z\sim p_z}{\mathbb{E}} [\log{(1-D(G(z)))}]\)
There are four important variables when training this GAN
\(z\): the noise that will be input to the generator
\(G(z)\): the output of the generator, i.e. the samples that should approximate the real samples
\(D(G(z))\): the discriminator’s decision based on the fake sample
\(x\): real samples drawn from the real sample distribution
The generator \(G\) is trying to minimize the overall objective, and the discriminator \(D\) tries to maximize it. In other words, the discriminator aims to minimize the binary cross-entropy such that it predicts 1 for any real sample \(x\) and 0 for any fake sample \(G(z)\). At the same time, the generator tries to get the discriminator to predict 1 any fake sample \(G(z)\).
The cell below defines the optimizers for both networks. Note that while the networks share an objective function, they each have their own optimizer. We use the Adam optimizer in both cases, with the same settings. We use the stable BCEWithLogitsLoss loss function, that combines binary cross-entropy calculation with a sigmoid.
# Initialize both networks
discriminator = Discriminator_1D().to(device)
generator = Generator_1D().to(device)
# Configure optimizers and loss function
optimizer_dis = torch.optim.Adam(discriminator.parameters(), lr=0.0002, betas=(0.5, 0.999))
optimizer_gen = torch.optim.Adam(generator.parameters(), lr=0.0002, betas=(0.5, 0.999))
# We use the same loss function for both networks
loss_function = torch.nn.BCEWithLogitsLoss()
The code below will run the training loop. It’s a bit different then you’re used to, take a good look.
Exercise
In the lecture it was mentioned that the generator should be frozen when training the discriminator and vice versa. Do you see where this is happening?
In the block
for param in generator.parameters():
param.requires_grad = False
for param in discriminator.parameters():
param.requires_grad = True
and
for param in generator.parameters():
param.requires_grad = True
for param in discriminator.parameters():
param.requires_grad = False
Now run the cell. This could take a few minutes, but below the cell you will periodically see a plot of the current situation. The plot shows the fake and real data distribution and the discriminators predictions (in blue).
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import display, clear_output
# We will store the losses here
gen_losses = []
dis_losses = []
# Training loop
n_samples = 500
iterations = 10000
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
for iteration in range(1, iterations + 1):
# ========== Train Discriminator ==========
for param in generator.parameters():
param.requires_grad = False
for param in discriminator.parameters():
param.requires_grad = True
discriminator.zero_grad()
# Get a random set of input noise
noise = torch.normal(0, 1, size=(n_samples, latent_dim), device=device)
# Also get a sample from the 'real' distribution
real = torch.normal(real_mean, 1, size=(n_samples, latent_dim), device=device)
# Generate some fake samples using the generator
fake = generator(noise)
# Concatenate the fake and real images
dis_input = torch.cat((real, fake))
# Make labels for generated and real data (set labels for real samples to 1)
dis_labels = torch.zeros((2 * n_samples, latent_dim), device=device)
dis_labels[:n_samples] = 1
# Train discriminator with this batch of samples
predictions = discriminator(dis_input)
dis_loss = loss_function(predictions, dis_labels)
dis_loss.backward()
optimizer_dis.step()
dis_losses.append(dis_loss.detach().cpu().numpy())
# ========== Train Generator ==========
for param in generator.parameters():
param.requires_grad = True
for param in discriminator.parameters():
param.requires_grad = False
generator.zero_grad()
# Get a random set of input noise
noise = torch.normal(0, 1, size=(n_samples, latent_dim), device=device)
# From the generator's perspective, the discriminator should predict ones for all samples
gen_labels = torch.ones((n_samples, latent_dim), device=device)
# Train generator
fake = generator(noise)
predictions = discriminator(fake)
gen_loss = loss_function(predictions, gen_labels)
gen_loss.backward()
optimizer_gen.step()
gen_losses.append(gen_loss.detach().cpu().numpy())
# ========== Make plot ==========
# For every 100th iteration, plot samples from real and fake distributions
if iteration % 100 == 0:
# Generate fake samples and predictions without gradient calculations
with torch.no_grad():
# Get fake and real samples, together with discriminator predictions from a standard range of values
noise = torch.normal(0, 1, size=(n_samples, latent_dim), device=device)
fake = generator(noise)
real = torch.normal(real_mean, 1, size=(n_samples, latent_dim), device=device)
predictions = torch.sigmoid(discriminator(torch.arange(-20, 20, 0.5, device=device).view(80, 1)))
# Make new plot and sleep half a second
ax.cla()
ax.set(xlim=(-20, 20), ylim=(0, 1))
ax.hist((torch.squeeze(fake).cpu().numpy(), torch.squeeze(real).cpu().numpy()), density=True, stacked=True, color=('g','k'))
ax.scatter(np.arange(-20, 20, 0.5), predictions.cpu().numpy(), c='b')
ax.set_title('Iteration {}'.format(iteration))
ax.legend(['Discriminator', 'Fake', 'Real'])
display(fig)
clear_output(wait=True)
plt.pause(0.5)
If all is well, the fake and real distributions should overlap nicely after training. The discriminator has essentially pushed the fake samples towards the real distribution and the generator is now able to transform the noise distribution into a distribution of ‘real’ samples!
Exercise
Can you explain what happened to the blue line during training? Why does it look like it does after training?
Answer key
If all is well, the blue line becomes horizontal: the discriminator \(D\) predicts 0.5 for each sample. Hence, it can no longer distinguish between fake and real samples.
Exercise
Try training the GAN with different input noise distributions for \(z\), e.g. a uniform distribution. See if you can find a distribution for the real samples for which the generator fails to generate samples.
Answer key
In principle, a uniform distribution shouldn’t really be a problem. What could be a problem is if you move the distribution of real samples too far away from 0, by changing the real_mean parameter too much.
During training, we have stored the loss values for the discriminator and the generator. We can now plot these. In the neural networks that we’ve trained so far, we have tried to train a neural network such that the loss decreases until a minimum is reached.
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(dis_losses)
plt.title('Discriminator loss')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.subplot(1, 2, 2)
plt.plot(gen_losses)
plt.title('Generator loss')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.show()
Exercise
The loss curves that you get now look different. Can you explain why they’re not nicely dropping to zero? Can you explain the value in the loss in the discriminator based on the objective function of the discriminator? Consider that we actually let the discriminator optimize a binary cross-entropy loss.
Answer key
If all is well, both loss curves converge to \(-ln(0.5) ~ 0.69\). In binary cross-entropy, if the prediction is 0.5 for a sample for which the reference is either 0 or 1, the loss is \(-ln(0.5)\).
MNIST synthesis#
Although it is definitely nice that we can train two networks together to learn the distribution of a real data distribution, generating samples from a normal distribution is in itself not really interesting. Luckily, we can use the same principles to generate images. We will be synthesizing MNIST digits. To prepare for this, we first download the dataset. The code in this cell should look familiar:
We compose several transforms into one transform
The
torchvisionlibrary conveniently lets you generate aDatasetobject that already includes the MNIST digit dataset (and downloads it from the internet)The
DataLoaderis just what we have used before.
However, note that we do not use MONAI here, instead we use an original PyTorch DataLoader, which works in just the same way.
import torchvision
from torchvision.transforms import Compose, PILToTensor, ConvertImageDtype, Normalize
from torch.utils.data import DataLoader
# Define transform that converts PIL images into Tensors, with values between -1.0 and 1.0
transform = Compose([
PILToTensor(),
ConvertImageDtype(torch.float),
Normalize(mean=0.5, std=0.5)
])
# Load the MNIST dataset
mnist_data = torchvision.datasets.MNIST(root='datasets', download=True, transform=transform)
data_loader = DataLoader(mnist_data, batch_size=100, shuffle=True)
The below code gets a batch of samples from the MNIST dataset and let’s you plot these. These are the \(28\times 28\) pixel images that you will be synthesizing.
def plotImages(images, dim=(10, 10), figsize=(10, 10), title=''):
num_images = dim[0] * dim[1]
images = images.reshape((num_images, 28, 28))
fig = plt.figure(figsize=figsize)
fig.suptitle(title, fontsize=14)
for i in range(images.shape[0]):
plt.subplot(dim[0], dim[1], i+1)
plt.imshow(images[i], interpolation='nearest', cmap='gray_r')
plt.axis('off')
plt.tight_layout()
plt.show()
# Get first batch of images and plot them in a grid
images, labels = next(iter(data_loader))
plotImages(images.numpy(), title='MNIST examples')
Most deep learning tutorials build a discriminative model that is able to classify an image into one of the ten digit categories. In this exercise, we are going to do the inverse. Given a point in a latent space (which in our case will be a multi-dimensional Gaussian distribution), we are going to train the network to generate a realistic digit image for this point. The MNIST data set will be used as a set of real samples.
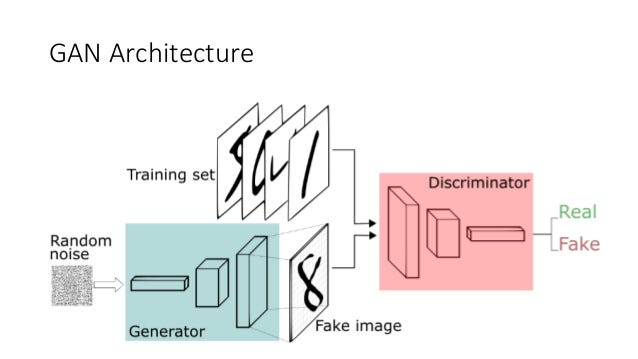
The discriminator#
As you can see in the image above, we will need a generator and a discriminator network. Let’s define these first using the cells below. First, we define the discriminator, which will classify images as either real or fake.
class Discriminator_MLP(nn.Module):
def __init__(self):
super(Discriminator_MLP, self).__init__()
self.layers = nn.Sequential(nn.Linear(in_features=784, out_features=1024),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Linear(in_features=1024, out_features=512),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Linear(in_features=512, out_features=256),
nn.LeakyReLU(0.2),
nn.Linear(in_features=256, out_features=1),
nn.Sigmoid())
def forward(self, x):
return self.layers(x)
Exercise
Is this a convolutional neural network? Why (not)?
Answer key
No, there’s no convolution layers.
You could argue that digits are a bit more complex than samples from a Gaussian distribution, so let’s set the latent space dimensionality for noise sampling a bit higher than 1. We will sample noise from a 10-dimensional distribution. It’s good to realize that this is still much lower than the 784 dimensions (28x28) that our original MNIST images have.
latent_dim = 10
The generator#
The generator is different than the discriminator. It should go from a low-dimensional noise vector to an MNIST image.
class Generator_MLP(nn.Module):
def __init__(self):
super(Generator_MLP, self).__init__()
self.layers = nn.Sequential(nn.Linear(in_features=latent_dim, out_features=256),
nn.LeakyReLU(0.2),
nn.Linear(in_features=256, out_features=512),
nn.LeakyReLU(0.2),
nn.Linear(in_features=512, out_features=1024),
nn.LeakyReLU(0.2),
nn.Linear(in_features=1024, out_features=784),
nn.Tanh())
def forward(self, x):
return self.layers(x)
Exercise
Consider the activation functions of the output layers of the generator and discriminator networks. How are they different?
Answer key
The generator has a Tanh output, which means that all output values will be squashed between -1 and 1. The discriminator has a sigmoid output because it performs classification.
The model#
Now let’s combine the generator and the discriminator. We train both using a binary cross-entropy objective. This is very similar to what we did before.
# Get networks
discriminator = Discriminator_MLP()
generator = Generator_MLP()
# Push networks to device
discriminator.to(device)
generator.to(device)
# Configure optimizers and loss function
optimizer_dis = torch.optim.Adam(discriminator.parameters(), lr=0.0002, betas=(0.5, 0.999))
optimizer_gen = torch.optim.Adam(generator.parameters(), lr=0.0002, betas=(0.5, 0.999))
loss = torch.nn.BCELoss()
We define some helper functions that will allow us to save and plot the models.
# Save model checkpoint in a folder called 'saved_models'
def saveModels(epoch, model_name):
to_save = {
'epoch': epoch,
'generator': generator.state_dict(),
'discriminator': discriminator.state_dict(),
'optimizer_gen': optimizer_gen.state_dict(),
'optimizer_dis': optimizer_dis.state_dict()
}
directory = os.path.join('saved_models', model_name)
if not os.path.exists(directory):
os.makedirs(directory)
torch.save(to_save, os.path.join(directory, 'Epoch_{}.pt'.format(epoch)))
# Plot generated images in a grid
def plotGeneratedImages(epoch, examples=100, dim=(10, 10), figsize=(10, 10)):
with torch.no_grad():
noise = torch.normal(0, 1, size=(examples, latent_dim), device=device)
fake_images = generator(noise).cpu().numpy()
fake_images = fake_images.reshape(examples, 28, 28)
fig = plt.figure(figsize=figsize)
fig.suptitle('Epoch {}'.format(epoch), fontsize=14)
for i in range(fake_images.shape[0]):
plt.subplot(dim[0], dim[1], i+1)
plt.imshow(fake_images[i], interpolation='nearest', cmap='gray_r')
plt.axis('off')
plt.tight_layout()
plt.show()
return fig
Exercise
Take a look at the code, it’s actually very similar to what we used in the first, 1D, GAN. See if you can find at least two differences.
If you run the code, synthesized images should be shown periodically.
Answer key
Some differences:
We use label smoothing now (the real samples get label 0.9 instead of 1.0). This makes it more difficult for the discriminator to distinguish fake from real images, and is used to make GANs train better.
The latent space dimensionality is larger
We flatten the images before they go into the discriminator
from tqdm import tqdm
import os
dis_losses = []
gen_losses = []
epochs = 20
batch_size = 100
fig = None
for epoch in range(1, epochs + 1):
# Wrap dataloader into tqdm such that we can print progress while training
with tqdm(data_loader, unit="iterations") as tqdm_iterator:
tqdm_iterator.set_description('Epoch {}'.format(epoch))
for i, batch in enumerate(tqdm_iterator):
# ========== Train Discriminator ==========
# Freeze generator part
for param in generator.parameters():
param.requires_grad = False
for param in discriminator.parameters():
param.requires_grad = True
discriminator.zero_grad()
# Get a random set of input noise
noise = torch.normal(0, 1, size=(batch_size, latent_dim), device=device)
# Get real images and flatten the image dimensions
real_images, _ = batch
real_images = real_images.to(device).view(batch_size, 784)
# Generate some fake MNIST images using the generator
fake_images = generator(noise)
# Concatenate the fake and real images
dis_input = torch.cat((real_images, fake_images))
# Labels for generated and real data
dis_labels = torch.zeros((2 * batch_size, 1), device=device)
# One-sided label smoothing
dis_labels[:batch_size] = 0.9
# Train discriminator with this batch of samples
predictions = discriminator(dis_input)
dis_loss = loss(predictions, dis_labels)
dis_loss.backward()
optimizer_dis.step()
dis_losses.append(dis_loss.detach().cpu().numpy())
# ========== Train Generator ==========
# Freeze the discriminator part
for param in generator.parameters():
param.requires_grad = True
for param in discriminator.parameters():
param.requires_grad = False
generator.zero_grad()
# Train generator with a new batch of generated samples
noise = torch.normal(0, 1, size=(batch_size, latent_dim), device=device)
# From the generator's perspective, the discriminator should predict
# ones for all samples
gen_labels = torch.ones((batch_size, 1), device=device)
# Train the GAN to predict ones
fake_images = generator(noise)
predictions = discriminator(fake_images)
gen_loss = loss(predictions, gen_labels)
gen_loss.backward()
optimizer_gen.step()
gen_losses.append(gen_loss.detach().cpu().numpy())
# Display generated images every 5th epoch
if epoch % 5 == 0:
clear_output(wait=True)
fig = plotGeneratedImages(epoch)
saveModels(epoch, 'MLP_GAN')
Exercise
If all is well, your model has synthesized images of digits. How cool is that?! Are you satisfied with the quality of these images? What could be improved?
Once again, we can plot the loss curves for the trained model.
Answer key
It’s likely that the synthesized images are still a bit noisy, this could be improved.
plt.figure(figsize=(10, 8))
plt.subplot(1, 2, 1)
plt.plot(dis_losses)
plt.title('Discriminator loss')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.subplot(1, 2, 2)
plt.plot(gen_losses)
plt.title('Generator loss')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.show()
Exercise
Inspect the loss curves for this model and explain what happens.
Answer key
Similarly to 1D synthesis, both loss terms converge to a value that indicates that the discriminator finds it hard to distinguish samples.
A convolutional model#
Thus far the discriminator and generator were both multilayer perceptrons. Now we’re going to add in some convolutional layers to turn them into a deep convolutional GAN (DCGAN)-like architecture. This means that we have to redefine the generator network and a discriminator network. First, we define the discriminator, which is a pretty basic classification CNN, similar to what you used in Tutorial 2.
class Discriminator_CNN(nn.Module):
def __init__(self):
super(Discriminator_CNN, self).__init__()
self.layers = nn.Sequential(nn.Conv2d(in_channels=1, out_channels=64, kernel_size=5, stride=2, padding=2),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Conv2d(in_channels=64, out_channels=128, kernel_size=5, stride=2, padding=2),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Flatten(),
nn.Linear(in_features=128*7*7, out_features=1),
nn.Sigmoid())
def forward(self, x):
return self.layers(x)
class Generator_CNN(nn.Module):
def __init__(self):
super(Generator_CNN, self).__init__()
self.linear = nn.Sequential(nn.Linear(in_features=latent_dim, out_features=128*7*7),
nn.LeakyReLU(0.2))
self.convolutional = nn.Sequential(nn.Upsample(size=(14, 14)),
nn.Conv2d(in_channels=128, out_channels=64, kernel_size=5, padding='same'),
nn.LeakyReLU(0.2),
nn.Upsample(size=(28, 28)),
nn.Conv2d(in_channels=64, out_channels=1, kernel_size=5, padding='same'),
nn.Tanh())
def forward(self, x):
x = self.linear(x)
x = x.view(-1, 128, 7, 7)
x = self.convolutional(x)
return x
Let’s build our GAN model like before.
# Get networks
discriminator = Discriminator_CNN()
generator = Generator_CNN()
# Push networks to device
discriminator.to(device)
generator.to(device)
# Configure optimizers and loss function
optimizer_dis = torch.optim.Adam(discriminator.parameters(), lr=0.0002, betas=(0.5, 0.999))
optimizer_gen = torch.optim.Adam(generator.parameters(), lr=0.0002, betas=(0.5, 0.999))
loss = torch.nn.BCELoss()
Train the model using the code below. Inspect the samples that come out.
Exercise
What are some differences between these samples and the ones generated by the multilayer perceptron GAN? Can you explain these differences?
Answer key
The samples generated with convolutional layers are likely to be more smooth/complete than the ones made with MLPs.
dis_losses = []
gen_losses = []
epochs = 50
batch_size = 100
for epoch in range(1, epochs + 1):
# Wrap dataloader into tqdm such that we can print progress while training
with tqdm(data_loader, unit="iterations") as tqdm_iterator:
tqdm_iterator.set_description('Epoch {}'.format(epoch))
for i, batch in enumerate(tqdm_iterator):
# ========== Train Discriminator ==========
# Freeze generator part
for param in generator.parameters():
param.requires_grad = False
for param in discriminator.parameters():
param.requires_grad = True
discriminator.zero_grad()
# Get a random set of input noise
noise = torch.normal(0, 1, size=(batch_size, latent_dim), device=device)
# Get real images and flatten the image dimensions
real_images, _ = batch
real_images = real_images.to(device)
# Generate some fake MNIST images using the generator
fake_images = generator(noise)
# Concatenate the fake and real images
dis_input = torch.cat((real_images, fake_images))
# Labels for generated and real data
dis_labels = torch.zeros((2 * batch_size, 1), device=device)
# One-sided label smoothing
dis_labels[:batch_size] = 0.9
# Train discriminator with this batch of samples
predictions = discriminator(dis_input)
dis_loss = loss(predictions, dis_labels)
dis_loss.backward()
optimizer_dis.step()
dis_losses.append(dis_loss.detach().cpu().numpy())
# ========== Train Generator ==========
# Freeze the discriminator part
for param in generator.parameters():
param.requires_grad = True
for param in discriminator.parameters():
param.requires_grad = False
generator.zero_grad()
# Train generator with a new batch of generated samples
noise = torch.normal(0, 1, size=(batch_size, latent_dim), device=device)
# From the generator's perspective, the discriminator should predict
# ones for all samples
gen_labels = torch.ones((batch_size, 1), device=device)
# Train the GAN to predict ones
fake_images = generator(noise)
predictions = discriminator(fake_images)
gen_loss = loss(predictions, gen_labels)
gen_loss.backward()
optimizer_gen.step()
gen_losses.append(gen_loss.detach().cpu().numpy())
# Every 5th epoch, display generated images and save model
if epoch % 5 == 0:
clear_output(wait=True)
plotGeneratedImages(epoch)
saveModels(epoch, 'CNN_GAN')
Interpolation in the latent space#
In the past two models, we have used a 10-dimensional latent space. We’re going to explore the content of this latent space a bit more. We randomly pick two points in the latent space and make a linear interpolation between these two points. Then we generate images from each of the interpolated latent points.
# Sample two points from noise distribution
noise_a = torch.normal(0, 1, size=(1, latent_dim), device=device)
noise_b = torch.normal(0, 1, size=(1, latent_dim), device=device)
# Interpolate in steps of 10% between the two points
noise = torch.zeros((10, latent_dim), dtype=torch.float, device=device)
for i in range(10):
ni = i * 0.1
noise[i, :] = ni * noise_a + (1 - ni) * noise_b
# Generate images from interpolated points
with torch.no_grad():
fake_images = generator(noise)
fake_images = fake_images.cpu().numpy()
plotImages(fake_images, dim=(1, 10), figsize=(10, 2), title='Generated images from interpolated points')
Exercise
Explain what you see in this figure.
Answer key
You should see a smooth(ish) interpolation between two randomly generated digits.
Exercise
Interpolation works, but what happens when you extrapolate out of the latent space distribution? Consider how the noise vectors are drawn. Inspect generated samples that are further away from the mode of your latent space.
Answer key
The further we move away from the mode of the noise distribution, the less realistic the samples become. The assumption in our model is that the samples follow a Gaussian distribution, and the generator will not know how to properly handle noise that is far away from the center.
MedMNIST image synthesis#
In this section, we’re going to synthesize images from MedMNIST. This is a collection of datasets with binary (yes or no) or multiclass labels in 2D or 3D. If you didn’t do it in Tutorial 2 you have to first install medmnist with the following commandline:
!pip install medmnist
As before, we can define a MedMNISTData class for these kinds of images.
import os
import monai
import torchvision.transforms as transforms
import medmnist
class MedMNISTData(monai.data.Dataset):
def __init__(self, datafile, transform=None):
self.data = datafile
self.transform = transform
def __getitem__(self, index):
# Make getitem return one tensor corresponding to the image
image = self.data[index][0]
if self.transform:
image = self.transform(image)
return image
def __len__(self):
return len(self.data)
data_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[.5], std=[.5])
])
dataset = medmnist.PneumoniaMNIST(split="train", download=True)
train_dataset = MedMNISTData(dataset, transform=data_transform)
train_loader = DataLoader(train_dataset, batch_size=10, shuffle=True)
Exercise
In this second-to-last part of the practical you’re going to repurpose the code that you have used so far to synthesize MedMNIST images. By now you should have sufficient experience with Python that you are able to fill in the block of code below and train your model. Reach out if you get stuck! Good luck!
Answer key
# Get networks
discriminator = Discriminator_CNN()
generator = Generator_CNN()
# Push networks to device
discriminator.to(device)
generator.to(device)
# Configure optimizers and loss function
optimizer_dis = torch.optim.Adam(discriminator.parameters(), lr=0.0002, betas=(0.5, 0.999))
optimizer_gen = torch.optim.Adam(generator.parameters(), lr=0.0002, betas=(0.5, 0.999))
loss = torch.nn.BCELoss()
dis_losses = []
gen_losses = []
epochs = 50
batch_size = 100
for epoch in range(1, epochs + 1):
# Wrap dataloader into tqdm such that we can print progress while training
with tqdm(train_loader, unit="iterations") as tqdm_iterator:
tqdm_iterator.set_description('Epoch {}'.format(epoch))
for i, batch in enumerate(tqdm_iterator):
# ========== Train Discriminator ==========
# Freeze generator part
for param in generator.parameters():
param.requires_grad = False
for param in discriminator.parameters():
param.requires_grad = True
discriminator.zero_grad()
# Get a random set of input noise
batch_size = len(batch)
noise = torch.normal(0, 1, size=(batch_size, latent_dim), device=device)
# Get real images and flatten the image dimensions
real_images = batch.to(device)
# Generate some fake MNIST images using the generator
with torch.no_grad():
fake_images = generator(noise)
# Concatenate the fake and real images
dis_input = torch.cat((real_images, fake_images))
# Labels for generated and real data
dis_labels = torch.zeros((2 * batch_size, 1), device=device)
# One-sided label smoothing
dis_labels[:batch_size] = 0.9
# Train discriminator with this batch of samples
predictions = discriminator(dis_input)
dis_loss = loss(predictions, dis_labels)
dis_loss.backward()
optimizer_dis.step()
dis_losses.append(dis_loss.detach().cpu().numpy())
# ========== Train Generator ==========
# Freeze the discriminator part
for param in generator.parameters():
param.requires_grad = True
for param in discriminator.parameters():
param.requires_grad = False
generator.zero_grad()
# Train generator with a new batch of generated samples
noise = torch.normal(0, 1, size=(batch_size, latent_dim), device=device)
# From the generator's perspective, the discriminator should predict
# ones for all samples
gen_labels = torch.ones((batch_size, 1), device=device)
# Train the GAN to predict ones
fake_images = generator(noise)
predictions = discriminator(fake_images)
gen_loss = loss(predictions, gen_labels)
gen_loss.backward()
optimizer_gen.step()
gen_losses.append(gen_loss.detach().cpu().numpy())
# Every 5th epoch, display generated images and save model
if epoch % 5 == 0:
clear_output(wait=True)
plotGeneratedImages(epoch)
saveModels(epoch, 'CNN_GAN')
```
Conditional MedMNIST synthesis#
Exercise
For all MedMMNIST samples we already have labels (0, 1, …, n). Try to change the MedMNIST synthesis code such that you can ask the generator to generate specific labels. I.e., try to train a conditional GAN. You can look for some inspiration in this paper, in particular Sec. 4.1. Remember that you already got the MedMNIST labels when loading the data set and you used them in Tutorial 2. You will have to add these labels to the discriminator and generator network. The easiest way is to just concatenate them to your input vectors.


